フェルマーの最終定理の証明問題が大学入試で出題されたら！？数学での得点の稼ぎ方。
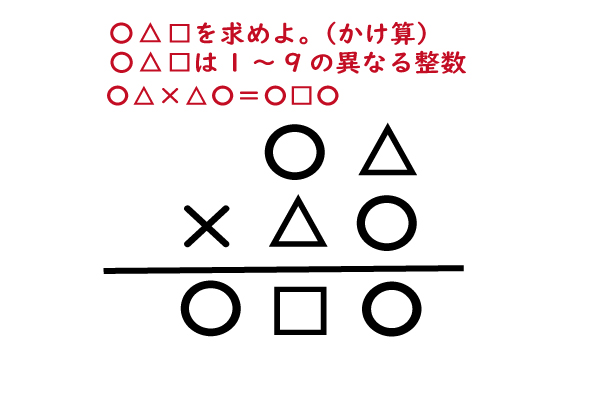
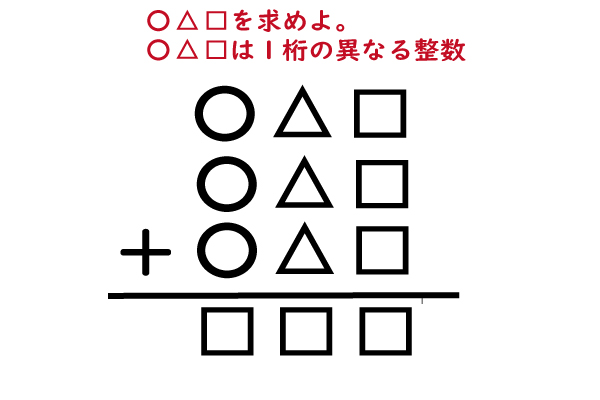
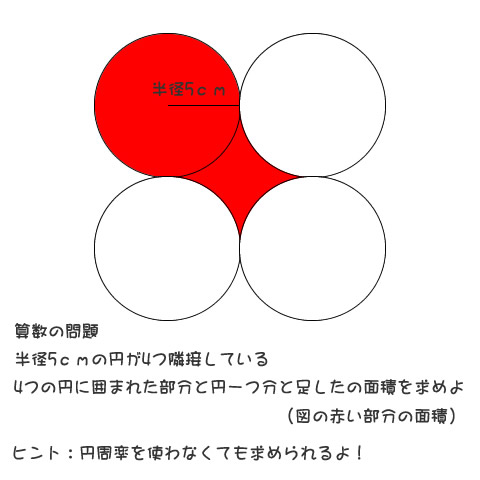
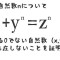先日の記事
フェルマーの最終定理
の証明問題です。
フェルマーの最終定理（フェルマーのさいしゅうていり、Fermat's Last Theorem）とは、
3 以上の自然数 n について、xn + yn = zn となる 0 でない自然数 (x, y, z) の組が存在しない
という定理のことである。
- フェルマーが驚くべき証明を得たと書き残したと伝えられる
- 長らく証明も反例もなされなかったことからフェルマー予想とも称された
- フェルマーの大定理とも呼ばれる。
- フェルマー予想が提起されてから360年後にアンドリュー・ワイルズによって完全に証明された
- ワイルズの定理あるいはフェルマー・ワイルズの定理とも呼ばれることがある
要するに360年間も証明されることのなかった難しい問題ということです。
フェルマーの最終定理の証明問題が大学入試で出題されたら！？
こんな問題が出題されることはまずないでしょうが、仮に出題されたとしても、その場であきらめてしまってはなりません。
全員が白紙で提出した場合、全員0点で差がつきませんが、実際はこんな問題でも｢部分点｣を稼ぐことはできます。
例えば
n=3,n=4のときこの定理が成り立つことを証明し
あとはnが素数のときにこの定理が成り立つことを証明すればよい。
といった方針を書くだけでもきっと部分点が貰える。
みんなが白紙の中、方針だけでも書けるかどうかが勝負の分かれ目となる。
実際の入試問題ではここまで難しい問題は出題されないが、自分にとってはフェルマーの最終定理と同じくらい難しいと感じる問題が出題されることがある。
そんな時でも白紙で提出するのではなく、
｢こういう風に解きたい！｣
という方針だけでも書いておくことが大学入試においては重要です。
白紙の答案にはどんなに頑張っても部分点をあげられません。
大学によって採点基準は違いますが、これを書けていたら何点といった細かな採点基準はありますので、必ず何かを書いて提出するようにしましょう。
みんなが解けないような難しい問題ほど、部分点の有無が勝敗を分けます。
フェルマーの最終定理の証明問題でも部分点は狙えるのですから、大学入試の問題で部分点をもらうくらい簡単なものです。
東大入試や京大入試に限らず、たまにとんでもなく難しい問題が出題されることがあります。
どんなに難しい問題が出題されても得点を稼げるようになりましょう。
関連記事
- 解けたら東大！？算数の問題。暗算でできるかな？円周率を使わずに求められます。
- ちんぷんかんぷん（珍糞漢糞）の意味と語源～答案を書く際に気をつけたいこと
- 京大受験数学の極意（理系）
- 補助線引けば秒殺！正六角形と台形の面積問題～小学生でも解ける問題です
