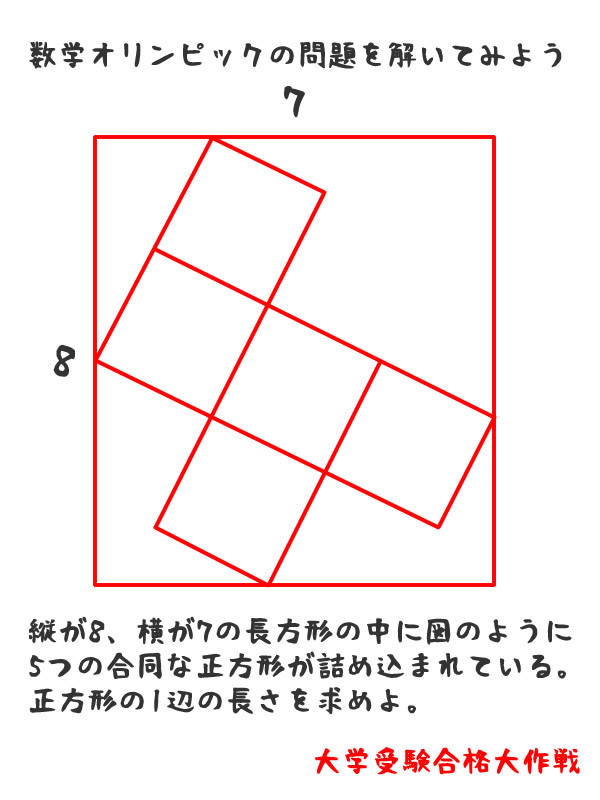
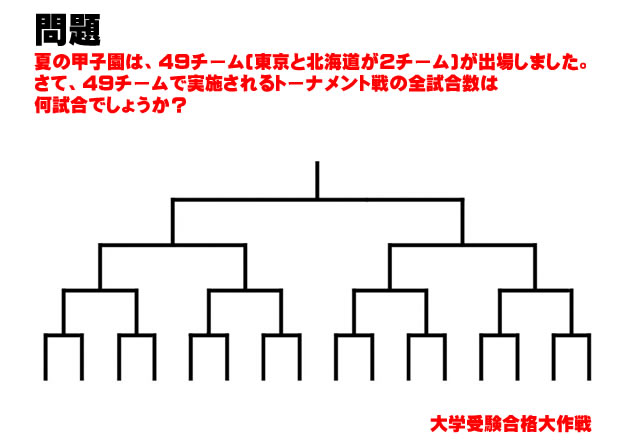
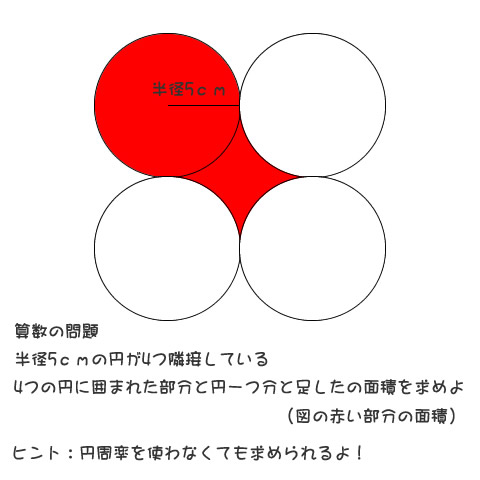
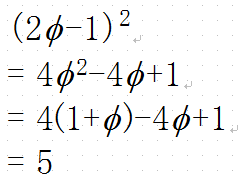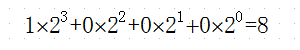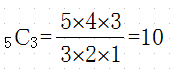文系にはわからない理系時計。理系でも解らないという声が多いので解説してみた。
1時
B'L とは「ルジャンドルの定数」(素数の頻度を表す公式に現れる定数)で19世紀前半には1.08366…と予想されていたのですが19期末にはちょうど「1」であると証明された
2時
無限等比級数の和
1+1/2+1/4+1/8+・・・・=2
3時
コレはhtmlの16進数文字コードで「3」を意味する。
4時
簡単に言うと1/2を7で割った余り。
もう少し説明すると
a≡a' (mod 7),b≡b' (mod 7)のとき
a+b≡a'+b' (mod 7)が成り立つので
(1/2) mod 7 ≡ (8/2) mod 7 ≡ 4 mod 7
ってことです。
(7で割った余りは1も8も同じ)
5時
φは黄金比と呼ばれ最も美しい比率とされている。
φ=(1+√5)/2
近似値は1.6180339887・・・黄金比には
という性質があるので
6時
コレは簡単3の階乗ですね。3!=3×2×1=6
7時
循環小数 6.99999・・・・・=7
8時
2進数で考えましょう
2進数の1000を10進数であらわすと
9時
10時
組み合わせ5C2のこと
11時
0Bは16進数の11
コンピューターで16進数の11を表記するとき 0×0Bで表現する
12時
1728の立方根(三乗根) 1728=12×12×12
ちなみに1728の次の整数 1729はハーディ=ラマヌジャン数と呼ばれ、「2 つの正の立方数の和として 2 通りの形で表すことのできる最小の数」である。
大学受験生なら
2,4,6,7,8,9,12
は解りたいところ。
5,10
も解れば数学の才能あります。というか数学好きな人でしょう。
3,11
は数学というより、プログラムの世界。
この時計は「理系向きの時計」「GeekClock」などと呼ばれています。
京大の素数ものさしと共に勉強机に備えてみるのはどうでしょうか?

お勧め記事